Physics Quest: The real valued, spatial symmetric represention of the electron and its spin.

20 Sep. 2012

The real symmetric representation of the Dirac equation.

by Hans de Vries

We describe how one can transform the standard representation of the Dirac equation into a new, spatially symmetric, real valued representation. It is shown that this new representation can be used as a direct replacement in QED and other standard model applications, it produces the same results and the notation is carefully chosen to be virtually identical to the standard notation.

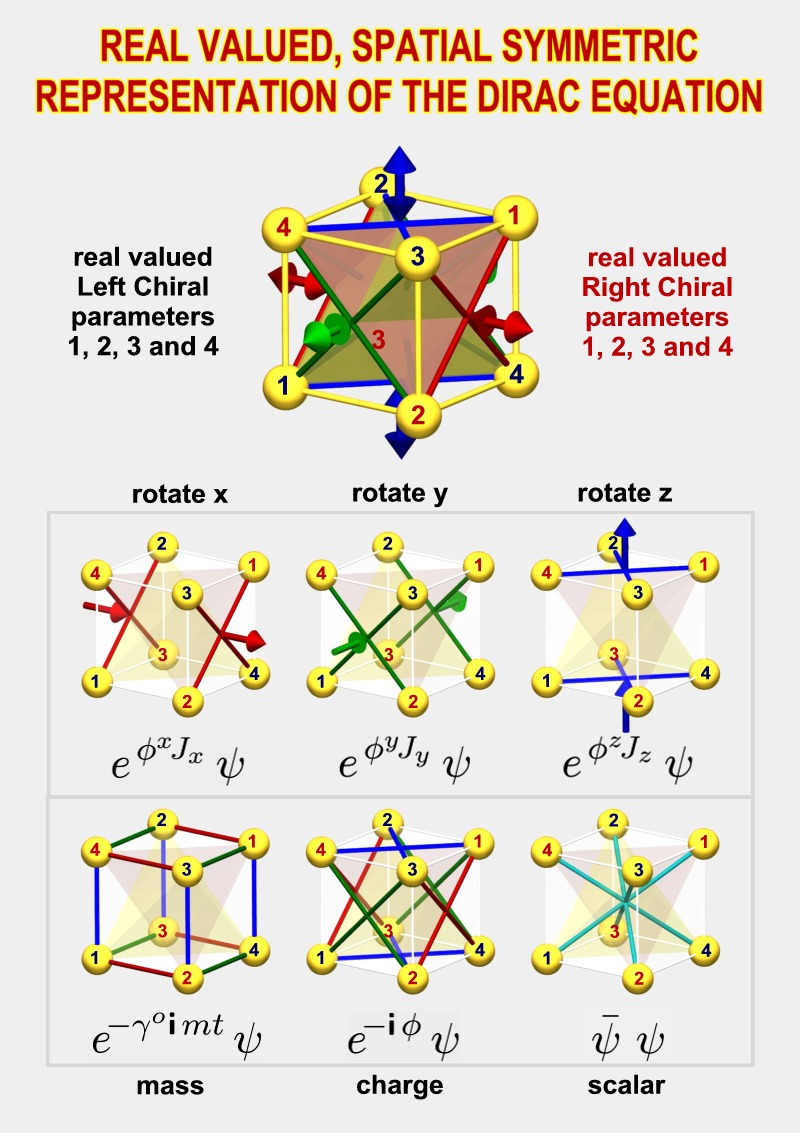
An overview of the real symmetric representation

The spatial symmetry of the 8 field parameters

One major consequence of the spatial symmetry is that the 8 field parameters get a spatial symmetric interpretation as well. The cube as seen in the illustrations occurs if we apply the so called "current" operator to the individual field parameters.

Each parameter becomes associated with a propagation (current)
from the center of the cube to one of the 8 vertices. Each of the 4 central axis of the cube has two of them, one is left circular polarized and the other is right circular polarized.

The eight parameters together define the direction of the electron's current density as well as the direction of the electron's spin.

Note that 4 axis-orientations are used to define directions instead of the usual 3 spatial coordinates. This means that there is a one parameter redundancy in the definitions. This redundant parameter turns out to be the phase of the wave function.

It's the phase of the wave function which enables the interference of matter waves. We have found a way in which nature can define a phase without needing a special preferred direction of rotation.

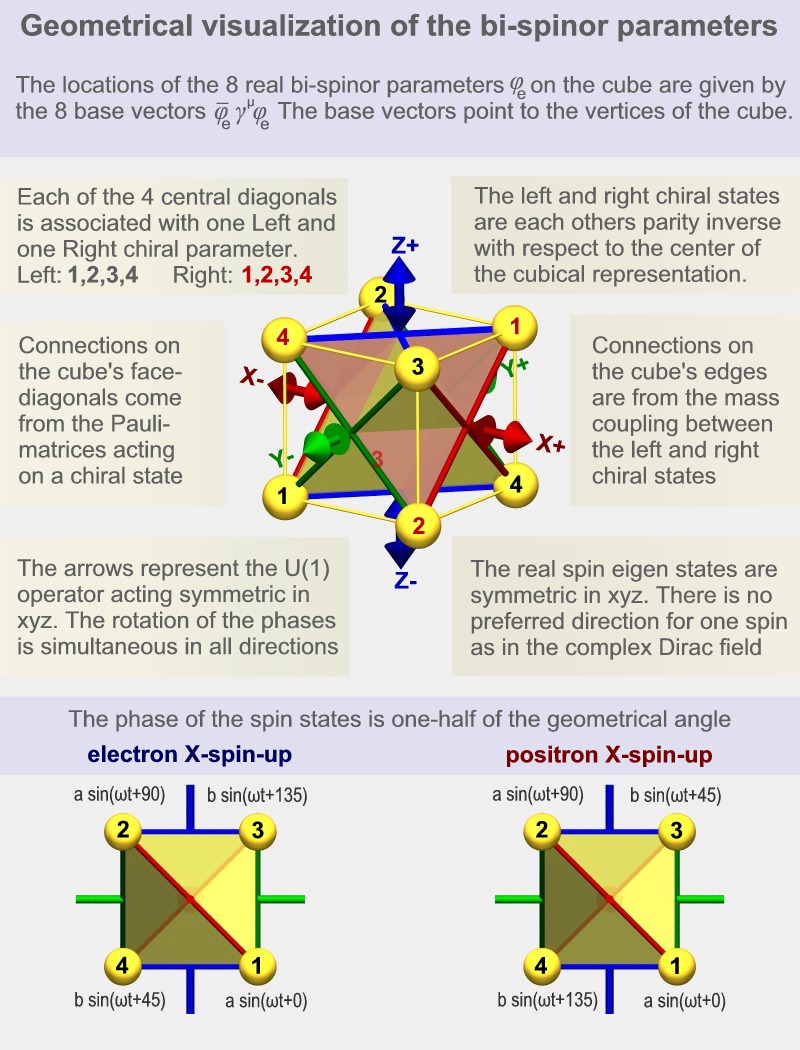
Overview

The 720 degrees of spinor rotation.

One of the most puzzling statements a student gets to hear is that
"an electron has to rotate over 720 degrees before it returns back
to its original position". This statement is directly related to another statement which says that the electron is a spin 1/2 particle.

All kinds of strange and often irrelevant visualizations are used by people who are trying to make sense of this. It turns out that we can find the mathematics corresponding to this spin 1/2 behavior directly in the representation itself.

We'll see that a more appropriate form of the 720 degrees statement is that "the phase difference is always 1/2 of the geometrical angle"

The electron and positron eigenstates.

We can calculate the eigenstates of the electron (and the positron) directly from the equation of motion. The particles oscillate with a frequency proportional to their mass. If we look at the parameters along, for instance, the x-axis (in case of a spin in the x direction) then we see that there are 45 degrees phase relations between parameters that are 90 degrees rotated from each other.

The images above show 4 parameters with phase shifts of 0, 45, 90 and 135 degrees. The other 4 parameters (in the positron case) have phase shifts of 180, 225, 270 and 315 degrees. In the case of the electron there are extra signs. This is what distinguishes the negative charge from the positive charge.

The real symmetric matrices of the representation

The rotation generators of spin 1/2 particles.

We can find the mathematical origin of this spin 1/2 behavior (or 720 degrees behavior) directly in the matrices used in the representation.
We can rotate the current and spin direction of the electron field with the use of the x, y and z-rotation matrices shown below.

Generally when we perform a continuous rotation then we operate on two (orthogonal) components so that these get a 90 degrees sine-cosine relation. The result is then a circular motion. In the real, symmetric representation however we operate on two parameters which are not orthogonal (90 degrees) but diagonally positioned
(180 degrees). The result is that the phase difference is 1/2 of the geometrical angle as is typical for a spin 1/2 particle

One can see that each rotation matrix defines four such connections, each time between two parameters. This is why there are four lines shown in each of the images (two X's) The signs in the matrices are so that all four rotations are defined as being in the same direction.

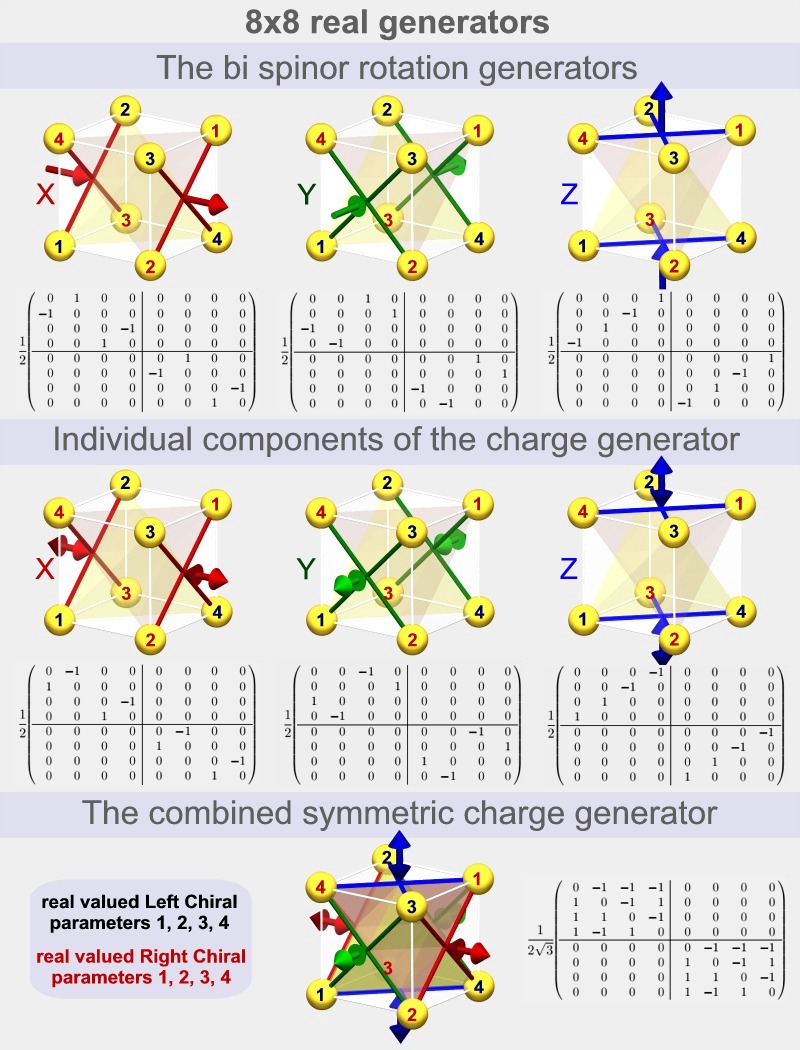
The charge generators of spin 1/2 particles.

If we place the electron in a potential field then its phase change rate will become higher if the electron's energy becomes higher and lower when the energy becomes lower.

If we rotate an electron then we will also change the phase of the parameters (by 1/2 the rate). However if we give the electron a different phase change rate by placing it in a constant potential field then we won't rotate the direction of the spin or the current, now, what is the difference mathematically?

We see in the image below that the individual components of the charge generator (which is used to describe the influence of the potential field) are almost identical to the rotation generators. The difference is in the signs. Two of the four connections are now opposite in sign. The result is that the net rotation is zero. The complete charge generator shown at the bottom is symmetric in x, y
and z: The electric potential field has no preferred direction in space.

HJkh

The boost generators of spin 1/2 particles.

If we boost a particle then we accelerate the particle to a different speed. The matrices used for this operation are the boost matrices.
These matrices are somewhat more complex but from the images we can see that they correspond to the x, y and z-directions.

The most important difference with the rotation matrices is that they are non-zero on the diagonals. This causes some parameters to become bigger and bigger when the boost becomes larger, while other parameters become smaller and smaller.

the +1's found on the diagonals correspond to the increasing parameters and the -1's correspond to decreasing parameters.

The parameters that become bigger are drawn with lighter colors while the ones that become smaller are darker. Now, each parameter corresponds with a current in its direction, from the center of the cube outward.

If we boost the electron in a certain direction then we indeed expect the currents in that direction to increase while the currents in the opposite direction should decrease.

The mass coupling of the chiral states.

If we don't place the electron in a potential field then we still expect that its phase changes continuously and it should do so with a frequency proportional to its mass.

The matrix which is responsible for this is the "mass coupling" matrix. This is the matrix which couples the four left chiral parameters with the four right chiral parameters. It is the only matrix which does so.

If we compare the 3 individual components of the mass coupling below with the 3 individual components of the charge generator above, then we see that they have the same 4x4 sub matrices
but in different quadrants.

This means that the mass coupling has the same effect as the charge generator when the four left chiral parameters are equal to the four right chiral parameters, and the opposite effect if there is a minus sign between the two chiral sets. This is the case in the electron and positron eigenstates respectively.

The combined mass coupling matrix is symmetric in x, y and z.
Mass does not have a preferred direction in space just like charge doesn't have a preferred direction.

About the PDF

The PDF was written over a period of about 3 years. It contains an overview in chapter 1 plus a complete step by step derivation of the real symmetric representation from the standard asymmetric complex one in chapter 2.

A lot of attention was spend at the development of the notation. The final form is highly compatible with the standard notation so that most expressions will be either the same or almost identical.The reader will be able to switch between the representations without effort.

The real symmetric representaion is obtained by going from the standard complex 2x2 Pauli matrices to their equivalent 4x4 real versions. The extra degrees of freedom obtained make it possible to make the representation symmetric.

The consequence of the 4x4 matrices is that SO(4) becomes the group of unitary generators of rotation and charge. The non-Abelian
charges introduced are discussed in chapter 3. Further chapters are
under development.